Why Science?
By Edward DienerUniversity of Utah, University of Virginia
Scientific research has been one of the great drivers of progress in human history, and the dramatic changes we have seen during the past century are due primarily to scientific findings—modern medicine, electronics, automobiles and jets, birth control, and a host of other helpful inventions. Psychologists believe that scientific methods can be used in the behavioral domain to understand and improve the world. Although psychology trails the biological and physical sciences in terms of progress, we are optimistic based on discoveries to date that scientific psychology will make many important discoveries that can benefit humanity. This module outlines the characteristics of the science, and the promises it holds for understanding behavior. The ethics that guide psychological research are briefly described. It concludes with the reasons you should learn about scientific psychology
Learning Objectives
- Describe how scientific research has changed the world.
- Describe the key characteristics of the scientific approach.
- Discuss a few of the benefits, as well as problems that have been created by science.
- Describe several ways that psychological science has improved the world.
- Describe a number of the ethical guidelines that psychologists follow.
Scientific Advances and World Progress
There are many people who have made positive contributions to humanity in modern times. Take a careful look at the names on the following list. Which of these individuals do you think has helped humanity the most?
- Mother Teresa
- Albert Schweitzer
- Edward Jenner
- Norman Borlaug
- Fritz Haber
The usual response to this question is “Who on earth are Jenner, Borlaug, and Haber?” Many people know that Mother Teresa helped thousands of people living in the slums of Kolkata (Calcutta). Others recall that Albert Schweitzer opened his famous hospital in Africa and went on to earn the Nobel Peace Prize. The other three historical figures, on the other hand, are far less well known. Jenner, Borlaug, and Haber were scientists whose research discoveries saved millions, and even billions, of lives. Dr. Edward Jenner is often considered the “father of immunology” because he was among the first to conceive of and test vaccinations. His pioneering work led directly to the eradication of smallpox. Many other diseases have been greatly reduced because of vaccines discovered using science—measles, pertussis, diphtheria, tetanus, typhoid, cholera, polio, hepatitis—and all are the legacy of Jenner. Fritz Haber and Norman Borlaug saved more than a billion human lives. They created the “Green Revolution” by producing hybrid agricultural crops and synthetic fertilizer. Humanity can now produce food for the seven billion people on the planet, and the starvation that does occur is related to political and economic factors rather than our collective ability to produce food.
If you examine major social and technological changes over the past century most of them can be directly attributed to science. The world in 1914 was very different than the one we see today (Easterbrook, 2003). There were few cars and most people traveled by foot, horseback, or carriage. There were no radios, televisions, birth control pills, artificial hearts or antibiotics. Only a small portion of the world had telephones, refrigeration or electricity. These days we find that 80% of all households have television and 84% have electricity. It is estimated that three quarters of the world’s population has access to a mobile phone! Life expectancy was 47 years in 1900 and 79 years in 2010. The percentage of hungry and malnourished people in the world has dropped substantially across the globe. Even average levels of I.Q. have risen dramatically over the past century due to better nutrition and schooling.
All of these medical advances and technological innovations are the direct result of scientific research and understanding. In the modern age it is easy to grow complacent about the advances of science but make no mistake about it—science has made fantastic discoveries, and continues to do so. These discoveries have completely changed our world.
What Is Science?
What is this process we call “science,” which has so dramatically changed the world? Ancient people were more likely to believe in magical and supernatural explanations for natural phenomena such as solar eclipses or thunderstorms. By contrast, scientifically minded people try to figure out the natural world through testing and observation. Specifically, science is the use of systematic observation in order to acquire knowledge. For example, children in a science class might combine vinegar and baking soda to observe the bubbly chemical reaction. These empirical methods are wonderful ways to learn about the physical and biological world. Science is not magic—it will not solve all human problems, and might not answer all our questions about behavior. Nevertheless, it appears to be the most powerful method we have for acquiring knowledge about the observable world. The essential elements of science are as follows:
-
Systematic observation is the core of science. Scientists observe the world, in a very organized way. We often measure the phenomenon we are observing. We record our observations so that memory biases are less likely to enter in to our conclusions. We are systematic in that we try to observe under controlled conditions, and also systematically vary the conditions of our observations so that we can see variations in the phenomena and understand when they occur and do not occur.

Systematic observation is the core of science. [Image: Cvl Neuro, https://goo.gl/Avbju7, CC BY-SA 3.0, https://goo.gl/uhHola] - Observation leads to hypotheses we can test. When we develop hypotheses and theories, we state them in a way that can be tested. For example, you might make the claim that candles made of paraffin wax burn more slowly than do candles of the exact same size and shape made from bee’s wax. This claim can be readily tested by timing the burning speed of candles made from these materials.
- Science is democratic. People in ancient times may have been willing to accept the views of their kings or pharaohs as absolute truth. These days, however, people are more likely to want to be able to form their own opinions and debate conclusions. Scientists are skeptical and have open discussions about their observations and theories. These debates often occur as scientists publish competing findings with the idea that the best data will win the argument.
- Science is cumulative. We can learn the important truths discovered by earlier scientists and build on them. Any physics student today knows more about physics than Sir Isaac Newton did even though Newton was possibly the most brilliant physicist of all time. A crucial aspect of scientific progress is that after we learn of earlier advances, we can build upon them and move farther along the path of knowledge.
Psychology as a Science
Even in modern times many people are skeptical that psychology is really a science. To some degree this doubt stems from the fact that many psychological phenomena such as depression, intelligence, and prejudice do not seem to be directly observable in the same way that we can observe the changes in ocean tides or the speed of light. Because thoughts and feelings are invisible many early psychological researchers chose to focus on behavior. You might have noticed that some people act in a friendly and outgoing way while others appear to be shy and withdrawn. If you have made these types of observations then you are acting just like early psychologists who used behavior to draw inferences about various types of personality. By using behavioral measures and rating scales it is possible to measure thoughts and feelings. This is similar to how other researchers explore “invisible” phenomena such as the way that educators measure academic performance or economists measure quality of life.
One important pioneering researcher was Francis Galton, a cousin of Charles Darwin who lived in England during the late 1800s. Galton used patches of color to test people’s ability to distinguish between them. He also invented the self-report questionnaire, in which people offered their own expressed judgments or opinions on various matters. Galton was able to use self-reports to examine—among other things—people’s differing ability to accurately judge distances.

Although he lacked a modern understanding of genetics Galton also had the idea that scientists could look at the behaviors of identical and fraternal twins to estimate the degree to which genetic and social factors contribute to personality; a puzzling issue we currently refer to as the “nature-nurture question.”
In modern times psychology has become more sophisticated. Researchers now use better measures, more sophisticated study designs and better statistical analyses to explore human nature. Simply take the example of studying the emotion of happiness. How would you go about studying happiness? One straightforward method is to simply ask people about their happiness and to have them use a numbered scale to indicate their feelings. There are, of course, several problems with this. People might lie about their happiness, might not be able to accurately report on their own happiness, or might not use the numerical scale in the same way. With these limitations in mind modern psychologists employ a wide range of methods to assess happiness. They use, for instance, “peer report measures” in which they ask close friends and family members about the happiness of a target individual. Researchers can then compare these ratings to the self-report ratings and check for discrepancies. Researchers also use memory measures, with the idea that dispositionally positive people have an easier time recalling pleasant events and negative people have an easier time recalling unpleasant events. Modern psychologists even use biological measures such as saliva cortisol samples (cortisol is a stress related hormone) or fMRI images of brain activation (the left pre-frontal cortex is one area of brain activity associated with good moods).
Despite our various methodological advances it is true that psychology is still a very young science. While physics and chemistry are hundreds of years old psychology is barely a hundred and fifty years old and most of our major findings have occurred only in the last 60 years. There are legitimate limits to psychological science but it is a science nonetheless.
Psychological Science is Useful
Psychological science is useful for creating interventions that help people live better lives. A growing body of research is concerned with determining which therapies are the most and least effective for the treatment of psychological disorders.

For example, many studies have shown that cognitive behavioral therapy can help many people suffering from depression and anxiety disorders (Butler, Chapman, Forman, & Beck, 2006; Hoffman & Smits, 2008). In contrast, research reveals that some types of therapies actually might be harmful on average (Lilienfeld, 2007).
In organizational psychology, a number of psychological interventions have been found by researchers to produce greater productivity and satisfaction in the workplace (e.g., Guzzo, Jette, & Katzell, 1985). Human factor engineers have greatly increased the safety and utility of the products we use. For example, the human factors psychologist Alphonse Chapanis and other researchers redesigned the cockpit controls of aircraft to make them less confusing and easier to respond to, and this led to a decrease in pilot errors and crashes.
Forensic sciences have made courtroom decisions more valid. We all know of the famous cases of imprisoned persons who have been exonerated because of DNA evidence. Equally dramatic cases hinge on psychological findings. For instance, psychologist Elizabeth Loftus has conducted research demonstrating the limits and unreliability of eyewitness testimony and memory. Thus, psychological findings are having practical importance in the world outside the laboratory. Psychological science has experienced enough success to demonstrate that it works, but there remains a huge amount yet to be learned.
Ethics of Scientific Psychology
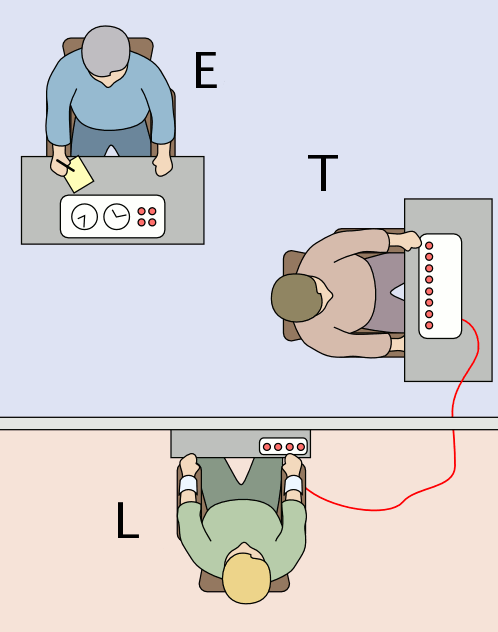
Psychology differs somewhat from the natural sciences such as chemistry in that researchers conduct studies with human research participants. Because of this there is a natural tendency to want to guard research participants against potential psychological harm. For example, it might be interesting to see how people handle ridicule but it might not be advisable to ridicule research participants.
Scientific psychologists follow a specific set of guidelines for research known as a code of ethics. There are extensive ethical guidelines for how human participants should be treated in psychological research (Diener & Crandall, 1978; Sales & Folkman, 2000). Following are a few highlights:
- Informed consent. In general, people should know when they are involved in research, and understand what will happen to them during the study. They should then be given a free choice as to whether to participate.
- Confidentiality. Information that researchers learn about individual participants should not be made public without the consent of the individual.
- Privacy. Researchers should not make observations of people in private places such as their bedrooms without their knowledge and consent. Researchers should not seek confidential information from others, such as school authorities, without consent of the participant or his or her guardian.
- Benefits. Researchers should consider the benefits of their proposed research and weigh these against potential risks to the participants. People who participate in psychological studies should be exposed to risk only if they fully understand these risks and only if the likely benefits clearly outweigh the risks.
- Deception. Some researchers need to deceive participants in order to hide the true nature of the study. This is typically done to prevent participants from modifying their behavior in unnatural ways. Researchers are required to “debrief” their participants after they have completed the study. Debriefing is an opportunity to educate participants about the true nature of the study.
Why Learn About Scientific Psychology?
I once had a psychology professor who asked my class why we were taking a psychology course. Our responses give the range of reasons that people want to learn about psychology:
- To understand ourselves
- To understand other people and groups
- To be better able to influence others, for example, in socializing children or motivating employees
- To learn how to better help others and improve the world, for example, by doing effective psychotherapy
- To learn a skill that will lead to a profession such as being a social worker or a professor
- To learn how to evaluate the research claims you hear or read about
- Because it is interesting, challenging, and fun! People want to learn about psychology because this is exciting in itself, regardless of other positive outcomes it might have. Why do we see movies? Because they are fun and exciting, and we need no other reason. Thus, one good reason to study psychology is that it can be rewarding in itself.
Conclusions
The science of psychology is an exciting adventure. Whether you will become a scientific psychologist, an applied psychologist, or an educated person who knows about psychological research, this field can influence your life and provide fun, rewards, and understanding. My hope is that you learn a lot from the modules in this e-text, and also that you enjoy the experience! I love learning about psychology and neuroscience, and hope you will too!
Outside Resources
- Web: Science Heroes- A celebration of people who have made lifesaving discoveries.
- http://www.scienceheroes.com/index.php?option=com_content&view=article&id=258&Itemid=27
Discussion Questions
- Some claim that science has done more harm than good. What do you think?
- Humanity is faced with many challenges and problems. Which of these are due to human behavior, and which are external to human actions?
- If you were a research psychologist, what phenomena or behaviors would most interest you?
- Will psychological scientists be able to help with the current challenges humanity faces, such as global warming, war, inequality, and mental illness?
- What can science study and what is outside the realm of science? What questions are impossible for scientists to study?
- Some claim that science will replace religion by providing sound knowledge instead of myths to explain the world. They claim that science is a much more reliable source of solutions to problems such as disease than is religion. What do you think? Will science replace religion, and should it?
- Are there human behaviors that should not be studied? Are some things so sacred or dangerous that we should not study them?
Vocabulary
- Empirical methods
- Approaches to inquiry that are tied to actual measurement and observation.
- Ethics
- Professional guidelines that offer researchers a template for making decisions that protect research participants from potential harm and that help steer scientists away from conflicts of interest or other situations that might compromise the integrity of their research.
- Hypotheses
- A logical idea that can be tested.
- Systematic observation
- The careful observation of the natural world with the aim of better understanding it. Observations provide the basic data that allow scientists to track, tally, or otherwise organize information about the natural world.
- Theories
- Groups of closely related phenomena or observations.
References
- Butler, A. C., Chapman, J. E., Forman, E. M., & Beck, A. T. (2006). The empirical status of cognitive-behavioral therapy: A review of meta-analyses. Clinical Psychology Review, 26, 17–31.
- Diener, E., & Crandall, R. (1978). Ethics in social and behavioral research. Chicago, IL: University of Chicago Press.
- Easterbrook, G. (2003). The progress paradox. New York, NY: Random House.
- Guzzo, R. A., Jette, R. D., & Katzell, R. A. (1985). The effects of psychologically based intervention programs on worker productivity: A meta-analysis. Personnel Psychology, 38, 275.291.
- Hoffman, S. G., & Smits, J. A. J. (2008). Cognitive-behavioral therapy for adult anxiety disorders. Journal of Clinical Psychiatry, 69, 621–32.
- Lilienfeld, S. O. (2007). Psychological treatments that cause harm. Perspectives on Psychological Science, 2, 53–70.
- Moore, D. (2003). Public lukewarm on animal rights. Gallup News Service, May 21. http://www.gallup.com/poll/8461/public-lukewarm-animal-rights.aspx
- Sales, B. D., & Folkman, S. (Eds.). (2000). Ethics in research with human participants. Washington, DC: American Psychological Association.
Authors
 Edward DienerEd Diener, Senior Scientist for the Gallup Organization and professor at the University of Virginia and University of Utah, received three of the highest honors in psychology (APA’s Distinguished Scientist Award, the APS William James Award, and election to the American Academy of Arts and Sciences) for his groundbreaking research on happiness.
Edward DienerEd Diener, Senior Scientist for the Gallup Organization and professor at the University of Virginia and University of Utah, received three of the highest honors in psychology (APA’s Distinguished Scientist Award, the APS William James Award, and election to the American Academy of Arts and Sciences) for his groundbreaking research on happiness.
Creative Commons License



 Why Science? by Edward Diener is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. Permissions beyond the scope of this license may be available in our Licensing Agreement.
Why Science? by Edward Diener is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. Permissions beyond the scope of this license may be available in our Licensing Agreement.