Aggression and Violence
By Brad J. BushmanThe Ohio State University
This module discusses the causes and consequences of human aggression and violence. Both internal and external causes are considered. Effective and ineffective techniques for reducing aggression are also discussed.
Learning Objectives
- Explain the important components of the definition of aggression, and explain how aggression differs from violence.
- Explain whether people think the world is less violent now than in the past, and whether it actually is less violent. If there is a discrepancy between perception and reality, how can it be resolved?
- Identify the internal causes and external causes of aggression. Compare and contrast how the inner and external causes differ.
- Identify effective and ineffective approaches to reducing aggression.
Introduction
"Beware of the dark side. Anger, fear, aggression; the dark side of the Force are they."
-Yoda, renowned Jedi master in the Star Wars universe
Aggression is indeed the dark side of human nature. Although aggression may have been adaptive in our ancient past, it hardly seems adaptive today. For example, on 14 December 2012 Adam Lanza, age 20, first killed his mother in their home, and then went to an elementary school in Newtown, Connecticut and began shooting, killing 20 children and 6 school employees, before killing himself. When incidents such as these happen, we want to know what caused them. Although it is impossible to know what motivated a particular individual such as Lanza to commit the Newtown school shooting, for decades researchers have studied the internal and external factors that influence aggression and violence. We consider some of these factors in this module.

Before we get too far, let’s begin by defining the term “aggression.” Laypeople and researchers often use the term “aggression” differently. Laypeople might describe a salesperson that tries really hard to sell them something as “aggressive.” The salesperson does not, however, want to harm potential customers. Most researchers define aggression as any behavior intended to harm another person who does not want to be harmed (Baron & Richardson, 1994). This definition includes three important features. First, aggression is a behavior—you can see it. Aggression is not an internal response, such as having angry feelings or aggressive thoughts (although such internal responses can increase the likelihood of actual aggression). Second, aggression is intentional rather than accidental. For example, a dentist might intentionally give a patient a shot of Novocain (which hurts!), but the goal is to help rather than harm the patient. Third, the victim wants to avoid the harm. Thus, suicide and sadomasochistic sex play would not be called aggression because the victim actively seeks to be harmed.
Researchers and laypeople also differ in their use of the term violence. A meteorologist might call a storm “violent” if it has intense winds, rain, thunder, lightning, or hail. Researchers define violence as aggression intended to cause extreme physical harm (e.g., injury, death). Thus, all violent acts are aggressive, but not all aggressive acts are violent. For example, screaming and swearing at another person is aggressive, but not violent.
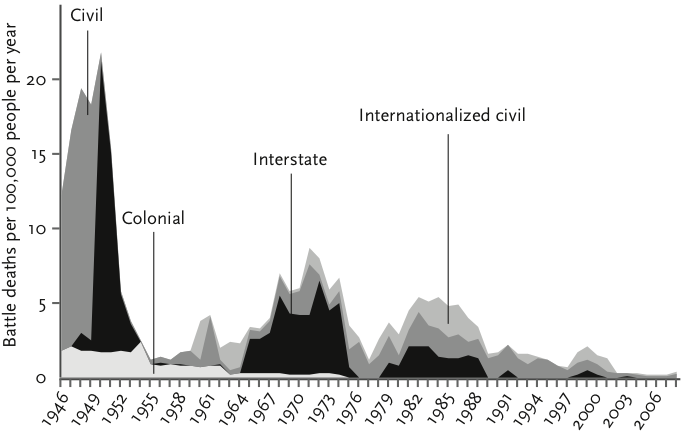
The good news is that the level of violence in the world is decreasing over time—by millennia, century, and even decade (Pinker, 2011). Studies of body counts, such as the proportion of prehistoric skeletons with axe and arrowhead wounds, suggest that prehistoric societies were far more violent than those today. Estimates show that if the wars of the 20th century had killed the same proportion of the population as ancient tribal wars did, then the death toll would have been 20 times higher—2 billion rather than 100 million. More recent data show that murder rates in Europe have decreased dramatically since the Middle Ages. For example, estimated murders in England dropped from 24 per 100,000 in the 14th century to 0.6 per 100,000 by the early 1960s. The major decline in violence occurred in the 17th century during the “Age of Reason,” which began in the Netherlands and England and then spread to other European countries. Global violence has also steadily decreased since the middle of the 20th century. For example, the number of battle deaths in interstate wars has declined from more than 65,000 per year in the 1950s to fewer than 2,000 per year in the 2000s. There have also been global declines in the number of armed conflicts and combat deaths, the number of military coups, and the number of deadly violence campaigns waged against civilians. For example, Figure 1 shows the number of battle deaths per 100,000 people per year over 60 years (see Pinker, 2011, p. 301). As can be seen, battle deaths of all types (civil, colonial, interstate, internationalized civil) have decreased over time. The claim that violence has decreased dramatically over time may seem hard to believe in today’s digital age when we are constantly bombarded by scenes of violence in the media. In the news media, the top stories are the most violent ones—“If it bleeds it leads,” so the saying goes. Citizen journalists around the world also use social media to “show and tell” the world about unjustified acts of violence. Because violent images are more available to us now than ever before, we incorrectly assume that violence levels are also higher. Our tendency to overestimate the amount of violence in the world is due to the availability heuristic, which is the tendency to judge the frequency or likelihood of an event by the ease with which relevant instances come to mind. Because we are frequently exposed to scenes of violence in the mass media, acts of violence are readily accessible in memory and come to mind easily, so we assume violence is more common than it actually is.
Human aggression is very complex and is caused by multiple factors. We will consider a few of the most important internal and external causes of aggression. Internal causes include anything the individual brings to the situation that increases the probability of aggression. External causes include anything in the environment that increases the probability of aggression. Finally, we will consider a few strategies for reducing aggression.
Internal Factors
Age
At what age are people most aggressive? You might be surprised to learn that toddlers 1 to 3 years old are most aggressive. Toddlers often rely on physical aggression to resolve conflict and get what they want. In free play situations, researchers have found that 25 percent of their interactions are aggressive (Tremblay, 2000). No other group of individuals (e.g., Mafia, street gangs) resorts to aggression 25 percent of the time. Fortunately for the rest of us, most toddler aggression isn’t severe enough to qualify as violence because they don’t use weapons, such as guns and knives. As children grow older, they learn to inhibit their aggressive impulses and resolve conflict using nonaggressive means, such as compromise and negotiation. Although most people become less aggressive over time, a small subset of people becomes more aggressive over time. The most dangerous years for this small subset of people (and for society as a whole) are late adolescence and early adulthood. For example, 18- to 24-year-olds commit most murders in the U.S. (U.S. Federal Bureau of Investigation, 2012).
Gender
At all ages, males tend to be more physically aggressive than females. However, it would be wrong to think that females are never physically aggressive. Females do use physical aggression, especially when they are provoked by other females (Collins, Quigley, & Leonard, 2007). Among heterosexual partners, women are actually slightly more likely than men to use physical aggression (Archer, 2000). However, when men do use physical aggression, they are more likely than women to cause serious injuries and even death to their partners. When people are strongly provoked, gender differences in aggression shrink (Bettencourt & Miller, 1996).
Females are much more likely than males to engage in relational aggression, defined as intentionally harming another person’s social relationships, feelings of acceptance, or inclusion within a group (Crick & Grotpeter, 1995). Examples of relational aggression include gossiping, spreading rumors, withdrawing affection to get what you want, excluding someone from your circle of friends, and giving someone the “silent treatment.”

Personality Traits Related to Aggression
Some people seem to be cranky and aggressive almost all the time. Aggressiveness is almost as stable as intelligence over time (Olweus, 1979). Individual differences in aggressiveness are often assessed using self-report questionnaires such as the “Aggression Questionnaire” (Buss & Perry, 1992), which includes items such as “I get into fights a little more than the average person” and “When frustrated, I let my irritation show.” Scores on these questionnaires are positively related to actual aggressive and violent behaviors (Anderson & Bushman, 1997).
The components of the “Dark Triad of Personality”—narcissism, psychopathy, and Machiavellianism—are also related to aggression (Paulhus & Williams, 2002). The term “narcissism” comes from the mythical Greek character Narcissus who fell in love with his own image reflected in the water. Narcissists have inflated egos, and they lash out aggressively against others when their inflated egos are threatened (e.g., Bushman & Baumeister, 1998). It is a common myth that aggressive people have low self-esteem (Bushman et al., 2009). Psychopaths are people who lack empathy for others. One of the strongest deterrents of aggression is empathy, which psychopaths lack. The term “Machiavellianism” comes from the Italian philosopher and writer Niccolò Machiavelli, who advocated using any means necessary to gain raw political power, including aggression and violence.
Hostile Cognitive Biases
One key to keeping aggression in check is to give people the benefit of the doubt. Some people, however, do just the opposite. There are three hostile cognitive biases. The hostile attribution bias is the tendency to perceive ambiguous actions by others as hostile actions (Dodge, 1980). For example, if a person bumps into you, a hostile attribution would be that the person did it on purpose and wants to hurt you. The hostile perception bias is the tendency to perceive social interactions in general as being aggressive (Dill et al., 1997). For example, if you see two people talking in an animated fashion, a hostile perception would be that they are fighting with each other. The hostile expectation bias is the tendency to expect others to react to potential conflicts with aggression (Dill et al., 1997). For example, if you bump into another person, a hostile expectation would be that the person will assume that you did it on purpose and will attack you in return. People with hostile cognitive biases view the world as a hostile place.
External Factors
Frustration and Other Unpleasant Events

One of the earliest theories of aggression proposed that aggression is caused by frustration, which was defined as blocking goal-directed behavior (Dollard et al., 1939). For example, if you are standing in a long line to purchase a ticket, it is frustrating when someone crowds in front of you. This theory was later expanded to say that all unpleasant events, not just frustrations, cause aggression (Berkowitz, 1989). Unpleasant events such as frustrations, provocations, social rejections, hot temperatures, loud noises, bad air (e.g., pollution, foul odors, secondhand smoke), and crowding can all cause aggression. Unpleasant events automatically trigger a fight–flight response.
Alcohol
Alcohol has long been associated with aggression and violence. In fact, sometimes alcohol is deliberately used to promote aggression. It has been standard practice for many centuries to issue soldiers some alcohol before they went into battle, both to increase aggression and reduce fear (Keegan, 1993). There is ample evidence of a link between alcohol and aggression, including evidence from experimental studies showing that consuming alcohol can cause an increase in aggression (e.g., Lipsey, Wilson, Cohen, & Derzon, 1997). Most theories of intoxicated aggression fall into one of two categories: (a) pharmacological theories that focus on how alcohol disrupts cognitive processes, and (b) expectancy theories that focus on how social attitudes about alcohol facilitate aggression. Normally, people have strong inhibitions against behaving aggressively, and pharmacological models focus on how alcohol reduces these inhibitions. To use a car analogy, alcohol increases aggression by cutting the brake line rather than by stepping on the gas. How does alcohol cut the brake line? Alcohol disrupts cognitive executive functions that help us organize, plan, achieve goals, and inhibit inappropriate behaviors (Giancola, 2000). Alcohol also reduces glucose, which provides energy to the brain for self-control (Gailliot & Baumeister, 2007). Alcohol has a “myopic” effect on attention—it causes people to focus attention only on the most salient features of a situation and not pay attention to more subtle features (Steele & Josephs, 1990). In some places where alcohol is consumed (e.g., crowded bar), provocations can be salient. Alcohol also reduces self-awareness, which decreases attention to internal standards against behaving aggressively (Hull, 1981).
According to expectancy theories, alcohol increases aggression because people expect it to. In our brains, alcohol and aggression are strongly linked together. Indeed, research shows that subliminally exposing people to alcohol-related words (e.g., vodka) can make them more aggressive, even though they do not drink one drop of alcohol (Subra et al., 2010). In many cultures, drinking occasions are culturally agreed-on “time out” periods where people are not held responsible for their actions (MacAndrew & Edgerton, 1969). Those who behave aggressively when intoxicated sometimes “blame the bottle” for their aggressive actions.
Does this research evidence mean that aggression is somehow contained in alcohol? No. Alcohol increases rather than causes aggressive tendencies. Factors that normally increase aggression (e.g., frustrations and other unpleasant events, aggressive cues) have a stronger effect on intoxicated people than on sober people (Bushman, 1997). In other words, alcohol mainly seems to increase aggression in combination with other factors. If someone insults or attacks you, your response will probably be more aggressive if you are drunk than sober. When there is no provocation, however, the effect of alcohol on aggression may be negligible. Plenty of people enjoy an occasional drink without becoming aggressive.
Reducing Aggression
Most people are greatly concerned about the amount of aggression in society. Aggression directly interferes with our basic needs of safety and security. Thus, it is urgent to find ways to reduce aggression. Because there is no single cause for aggression, it is difficult to design effective treatments. A treatment that works for one individual may not work for another individual. And some extremely aggressive people, such as psychopaths, are considered to be untreatable. Indeed, many people have started to accept the fact that aggression and violence have become an inevitable, intrinsic part of our society. This being said, there certainly are things that can be done to reduce aggression and violence. Before discussing some effective methods for reducing aggression, two ineffective methods need to be debunked: catharsis and punishment.
Catharsis
The term catharsis dates back to Aristotle and means to cleanse or purge. Aristotle taught that viewing tragic plays gave people emotional release from negative emotions. In Greek tragedy, the heroes didn’t just grow old and retire—they are often murdered. Sigmund Freud revived the ancient notion of catharsis by proposing that people should express their bottled-up anger. Freud believed if they repressed it, negative emotions would build up inside the individual and surface as psychological disorders. According to catharsis theory, acting aggressively or even viewing aggression purges angry feelings and aggressive impulses into harmless channels. Unfortunately for catharsis theory, research shows the opposite often occurs (e.g., Geen & Quanty, 1977).

If venting anger doesn’t get rid of it, what does? All emotions, including anger, consist of bodily states (e.g., arousal) and mental meanings. To get rid of anger, you can focus on either of those. Anger can be reduced by getting rid of the arousal state, such as by relaxing, listening to calming music, or counting to 10 before responding. Mental tactics can also reduce anger, such as by reframing the situation or by distracting oneself and turning one’s attention to more pleasant topics. Incompatible behaviors can also help get rid of anger. For example, petting a puppy, watching a comedy, kissing your lover, or helping someone in need, because those acts are incompatible with anger and, therefore, they make the angry state impossible to sustain (e.g., Baron, 1976). Viewing the provocative situation from a more distant perspective, such as that of a fly on the wall, also helps (Mischkowski, Kross, & Bushman, 2012).
Punishment
Most cultures assume that punishment is an effective way to deter aggression and violence. Punishment is defined as inflicting pain or removing pleasure for a misdeed. Punishment can range in intensity from spanking a child to executing a convicted killer. Parents use it, organizations use it, and governments use it, but does it work? Today, aggression researchers have their doubts. Punishment is most effective when it is: (a) intense, (b) prompt, (c) applied consistently and with certainty, (d) perceived as justified, and (e) possible to replace the undesirable punished behavior with a desirable alternative behavior (Berkowitz, 1993). Even if punishment occurs under these ideal conditions, it may only suppress aggressive behavior temporarily, and it has several undesirable long-term consequences. Most important, punishment models the aggressive behavior it seeks to prevent. Longitudinal studies have shown that children who are physically punished by their parents at home are more aggressive outside the home, such as in school (e.g., Lefkowitz, Huesmann, & Eron, 1978). Because punishment is unpleasant, it can also trigger aggression just like other unpleasant events.
Successful Interventions

Although specific aggression intervention strategies cannot be discussed in any detail here, there are two important general points to be made. First, successful interventions target as many causes of aggression as possible and attempt to tackle them collectively. Interventions that are narrowly focused at removing a single cause of aggression, however well conducted, are bound to fail. In general, external causes are easier to change than internal causes. For example, one can reduce alcohol consumption, and make unpleasant situations more tolerable (e.g., use air conditioners when it is hot, reduce crowding in stressful environments such as prisons and psychiatric wards).
Second, aggression problems are best treated in early development, when people are still malleable. As was mentioned previously, aggression is very stable over time, almost as stable as intelligence. If young children display excessive levels of aggression (often in the form of hitting, biting, or kicking), it places them at high risk for becoming violent adolescents and even violent adults. It is much more difficult to alter aggressive behaviors when they are part of an adult personality, than when they are still in development.
Yoda warned that anger, fear, and aggression are the dark side of the Force. They are also the dark side of human nature. Fortunately, aggression and violence are decreasing over time, and this trend should continue. We also know a lot more now than ever before about what factors increase aggression and how to treat aggressive behavior problems. When Luke Skywalker was going to enter the dark cave on Degobah (the fictional Star Wars planet), Yoda said, “Your weapons, you will not need them.” Hopefully, there will come a time in the not-too-distant future when people all over the world will no longer need weapons.
Outside Resources
- Book: Bushman, B. J., & Huesmann, L. R. (2010). Aggression. In S. T. Fiske, D. T. Gilbert, & G. Lindzey (Eds.), Handbook of social psychology (5th ed.) (pp. 833-863). New York: John Wiley & Sons.
- TED Talk: Zak Ebrahim
- https://www.ted.com/talks/zak_ebrahim_i_am_the_son_of_a_terrorist_here_s_how_i_chose_peace?language=en#t-528075
- Video: From the Inquisitive Mind website, Brad Bushman conducts a short review of terminology and important research concerning aggression and violence.
Discussion Questions
- Discuss whether different examples (hypothetical and real) meet the definition of aggression and the definition of violence.
- Consider the various causes of aggression described in this module and elsewhere, and discuss whether they can be changed to reduce aggression, and if so how.
Vocabulary
- Aggression
- Any behavior intended to harm another person who does not want to be harmed.
- Availability heuristic
- The tendency to judge the frequency or likelihood of an event by the ease with which relevant instances come to mind.
- Catharsis
- Greek term that means to cleanse or purge. Applied to aggression, catharsis is the belief that acting aggressively or even viewing aggression purges angry feelings and aggressive impulses into harmless channels.
- Hostile attribution bias
- The tendency to perceive ambiguous actions by others as aggressive.
- Hostile expectation bias
- The tendency to assume that people will react to potential conflicts with aggression.
- Hostile perception bias
- The tendency to perceive social interactions in general as being aggressive.
- Punishment
- Inflicting pain or removing pleasure for a misdeed. Punishment decreases the likelihood that a behavior will be repeated.
- Relational aggression
- Intentionally harming another person’s social relationships, feelings of acceptance, or inclusion within a group.
- Violence
- Aggression intended to cause extreme physical harm, such as injury or death.
References
- Anderson, C. A., & Bushman, B. J. (1997). External validity of “trivial” experiments: The case of laboratory aggression. Review of General Psychology, 1 (pp. 19-41).
- Archer, J. (2000). Sex differences in aggression between heterosexual partners: A meta-analytic review. Psychological Bulletin, 126 (pp. 651-680).
- Baron, R. A. (1976). The reduction of human aggression: A field study of the influence of incompatible reactions. Journal of Applied Social Psychology, 6 (pp. 260-274).
- Baron, R. A., & Richardson, D. R. (1994). Human aggression (2nd ed.). New York: Plenum Press.
- Berkowitz, L. (1989). Frustration-aggression hypothesis: Examination and reformulation. Psychological Bulletin, 106, 59-73.
- Bettencourt, B. A., & Miller, N. (1996). Gender differences in aggression as a function of provocation: A meta-analysis. Psychological Bulletin, 119 (pp. 422-447).
- Bushman, B. J. (1997). Effects of alcohol on human aggression: Validity of proposed explanations. In D. Fuller, R. Dietrich, & E. Gottheil (Eds.), Recent developments in alcoholism: Alcohol and violence (Vol. 13) (pp. 227-243). New York: Plenum Press.
- Bushman, B. J., & Baumeister, R. F. (1998). Threatened egotism, narcissism, self-esteem, and direct and displaced aggression: Does self-love or self-hate lead to violence? Journal of Personality and Social Psychology, 75, 219-229.
- Bushman, B. J., Baumeister, R. F., Thomaes, S., Ryu, E., Begeer, S., & West, S. G. (2009). Looking again, and harder, for a link between low self-esteem and aggression. Journal of Personality, 77(2) (pp. 427-446).
- Buss, A. H., & Perry, M. (1992). The aggression questionnaire. Journal of Personality and Social Psychology, 63 (pp. 452-459).
- Collins, R. L., Quigley, B., Leonard, K. (2007). Women’s physical aggression in bars: An event-based examination of precipitants and predictors of severity. Aggressive Behavior, 33(4) (pp. 304-313).
- Crick, N. R., & Grotpeter, J. K. (1995). Relational aggression, gender, and social-psychological adjustment. Child Development, 66 (pp. 710-722).
- Dill, K. E., Anderson, C. A., Anderson, K. B., & Deuser, W. E. (1997). Effects of aggressive personality on social expectations and social perceptions. Journal of Research in Personality, 31 (pp. 272-292).
- Dodge, K. A. (1980). Social cognition and children’s aggressive behavior. Child Development, 51 (pp. 620-635).
- Dollard, J., Doob, L., Miller, N., Mowrer, O., & Sears, R. (1939). Frustration and aggression. New Haven, CT: Yale University Press.
- Gailliot, M. T., & Baumeister, R. F. (2007). The physiology of willpower: Linking blood glucose to self-control. Personality and Social Psychology Review, 11(4) (pp. 303-327).
- Geen, R. G. & Quanty M. B. (1977). The catharsis of aggression: An evaluation of a hypothesis. In L. Berkowitz (Ed.), Advances in experimental social psychology (Vol. 10) (pp. 1-37). New York: Academic Press.
- Giancola, P. R. (2000). Executive functioning: A conceptual framework for alcohol-related aggression. Experimental Clinical Psychopharmacology, 8 (pp. 576-597).
- Hull, J. G. (1981). A self-awareness model of the causes and effects of alcohol consumption. Journal of Abnormal Psychology, 90 (pp. 586-600).
- Human Security Report Project (2007). Human Security Brief 2007. Vancouver, B.C., Canada: Human Security Report Project
- Keegan, J. (1993). A history of warfare. New York: Knopf.
- Lacina, B., & Gleditsch, N. P. (2005). Monitoring trends in global conflict: A new database in battle deaths. European Journal of Population, 21, 145-166.
- Lefkowitz, M. M., Huesmann, L. R., & Eron, L. D. (1978). Parental punishment: A longitudinal analysis of effects. Archives of General Psychiatry, 35(2), 186-191.
- Lipsey, M. W., Wilson, D. B., Cohen M. A., & Derzon, J. H. (1997). Is there a causal relationship between alcohol use and violence? A synthesis of the evidence. In M. Galanter (Ed.), Recent developments in alcoholism: Vol. 13. Alcohol and violence: Epidemiology, neurobiology, psychology, and family issues, (pp. 245-282). New York: Plenum Press.
- MacAndrew, C., & Edgerton, R. (1969). Drunken comportment: A social explanation. Chicago: Aldine.
- McEvedy, C., & Jones, R. (1978). Atlas of world population history. London: A. Lane.
- Mischkowski, D., Kross, E., & Bushman, B. J. (2012). Flies on the wall are less aggressive: Self-distanced reflection reduces angry feelings, aggressive thoughts, and aggressive behaviors. Journal of Experimental Social Psychology, 48, 1187-1191.
- Olweus, D. (1979). The stability of aggressive reaction patterns in males: A review. Psychological Bulletin, 86, 852-875.
- Paulhus, D. L, & Williams, K. M. (2002). The dark triad of personality: Narcissism, Machiavellianism, and psychopathy. Journal of Research in Personality, 36(6) (pp. 556-563).
- Pinker, S. (2011). The better angels of our nature. New York: Viking.
- Steele, C. M., & Josephs, R. A. (1990). Alcohol myopia: Its prized and dangerous effects. American Psychologist, 45 (pp. 921-933).
- Subra, B., Muller, D., Bègue, L., Bushman, B. J., & Delmas, F. (2010). Effects of alcohol and weapon cues on aggressive thoughts and behaviors. Personality and Social Psychology Bulletin, 36(8) (pp. 1052-1057).
- Tremblay, R. E. (2000). The development of aggressive behavior during childhood: What have we learned in the past century? International Journal of Behavioral Development, 24(2) (pp. 129-141).
- U.S. Census Bureau (2010). International data base (IDB): Total midyear population for the world: 1950-2020. http://www.census.gov/ipc/wwww/idb/worldpop.php
- U.S. Federal Bureau of Investigation. (2012). Uniform crime reports. Washington, DC: U.S. Government Printing Office.
Authors
 Brad J. BushmanBrad J. Bushman is a professor of communication and psychology at The Ohio State University, and a professor of communication science at the VU University, Amsterdam. For nearly 30 years he has studied the causes and consequences of human aggression. He has published nearly 150 peer-reviewed journal articles.
Brad J. BushmanBrad J. Bushman is a professor of communication and psychology at The Ohio State University, and a professor of communication science at the VU University, Amsterdam. For nearly 30 years he has studied the causes and consequences of human aggression. He has published nearly 150 peer-reviewed journal articles.
Creative Commons License



 Aggression and Violence by Brad J. Bushman is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. Permissions beyond the scope of this license may be available in our Licensing Agreement.
Aggression and Violence by Brad J. Bushman is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. Permissions beyond the scope of this license may be available in our Licensing Agreement.